This post is another in a series of posts saying that you shouldn’t always use the nice-looking version of an expression to calculate something. This post will look at the algorithm put forward by Paterson and Stockmeyer. The algorithm is useful for reducing the time complexity of evaluating polynomials of matrices since by reducing the number of matrix-matrix multiplication operations. This is done by effectively blocking the polynomial into sections. Visually it is simple to see what is happening. Here is an example in a $3^{rd}$ degree polynomial.
\[\begin{align*} f(X) &= a_0 + a_1X + a_2X^2 + a_3X^3\\ &= a_0 + a_1X + X^2(a_2 + a_3X) \end{align*}\]With this blocking structure in place, we only have to evaluate 2 matrix multiplications instead of 3. The results get more dramatic with larger degree polynomials, with scaling in the order of $\mathcal{O}(\sqrt{\text{degree}})$ instead of the algorithm based on caching the scales $\mathcal{O}(\text{degree})$, or $\mathcal{O}(\text{degree}^2)$ for the naive version.
The Wikipedia page describing it has a nice shorthand expression for this that looks like the following. ($k$ is the size of the blocks)
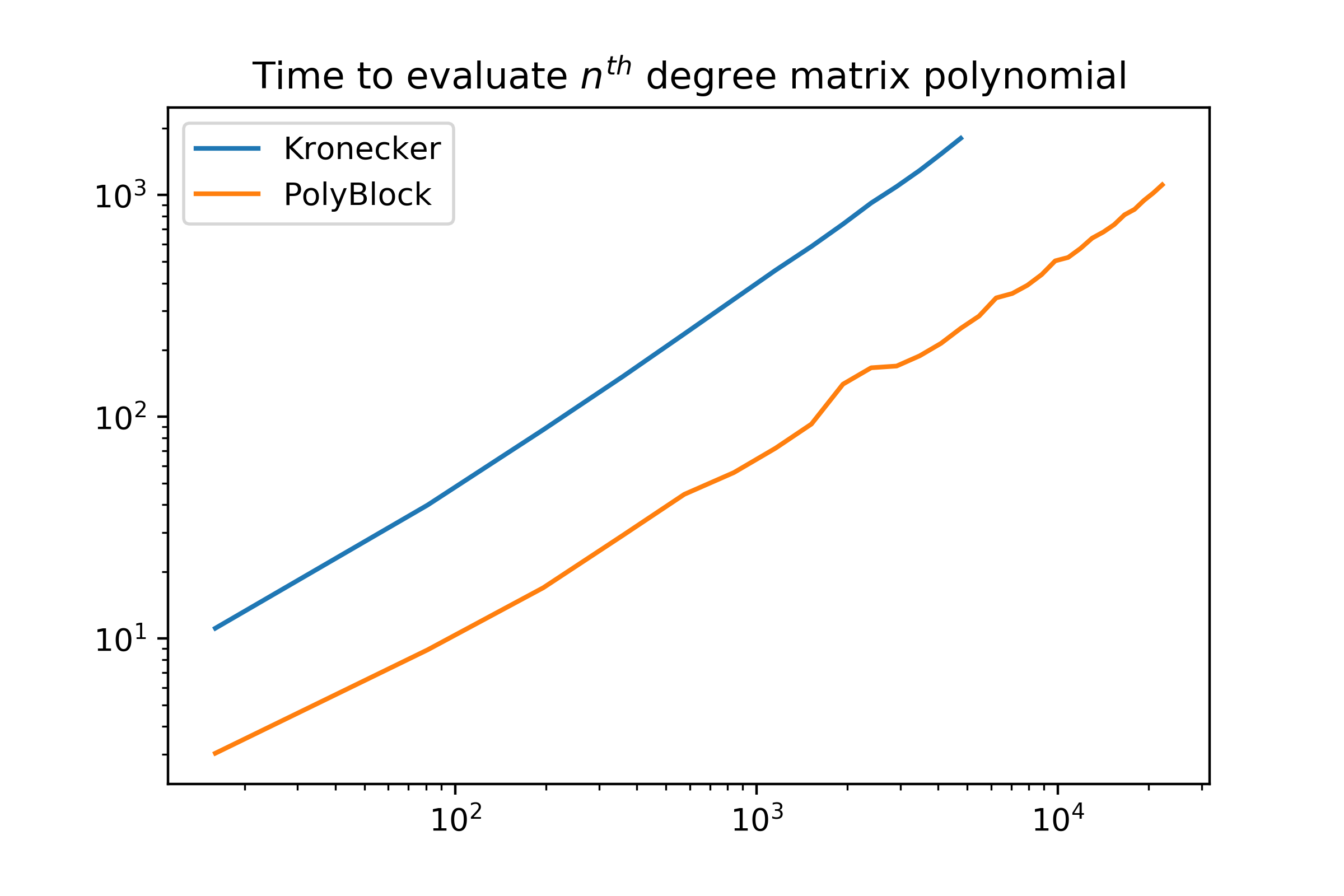
\[P(M) = \begin{bmatrix} I\\ M\\ \vdots\\ M^{k-1} \end{bmatrix}^T \left( \begin{bmatrix} a_0 & a_1 & a_2 & \dots \\ a_k & a_{k+1} & \ddots & \\ a_{2k} & \ddots &&\\ \vdots &&&\\ \end{bmatrix}\otimes I \right) \begin{bmatrix} I\\ M^k\\ M^{2k}\\ \vdots\\ \end{bmatrix}\]However, if you actually wanted to evaluate it, unlike the original algorithm, it is slower and takes asymptotically more memory. I implemented both in python and benchmarked them to look at the experimental time and space complexity with a polynomial $A\in\mathcal{R}^{200\times200}$ on the Taylor series of the matrix polynomial. We can see that while both algorithms scale similarly, the Kronecker-based expression is approximately 5 to 6 times slower than evaluating the blocked polynomial with an increasing gap over time.
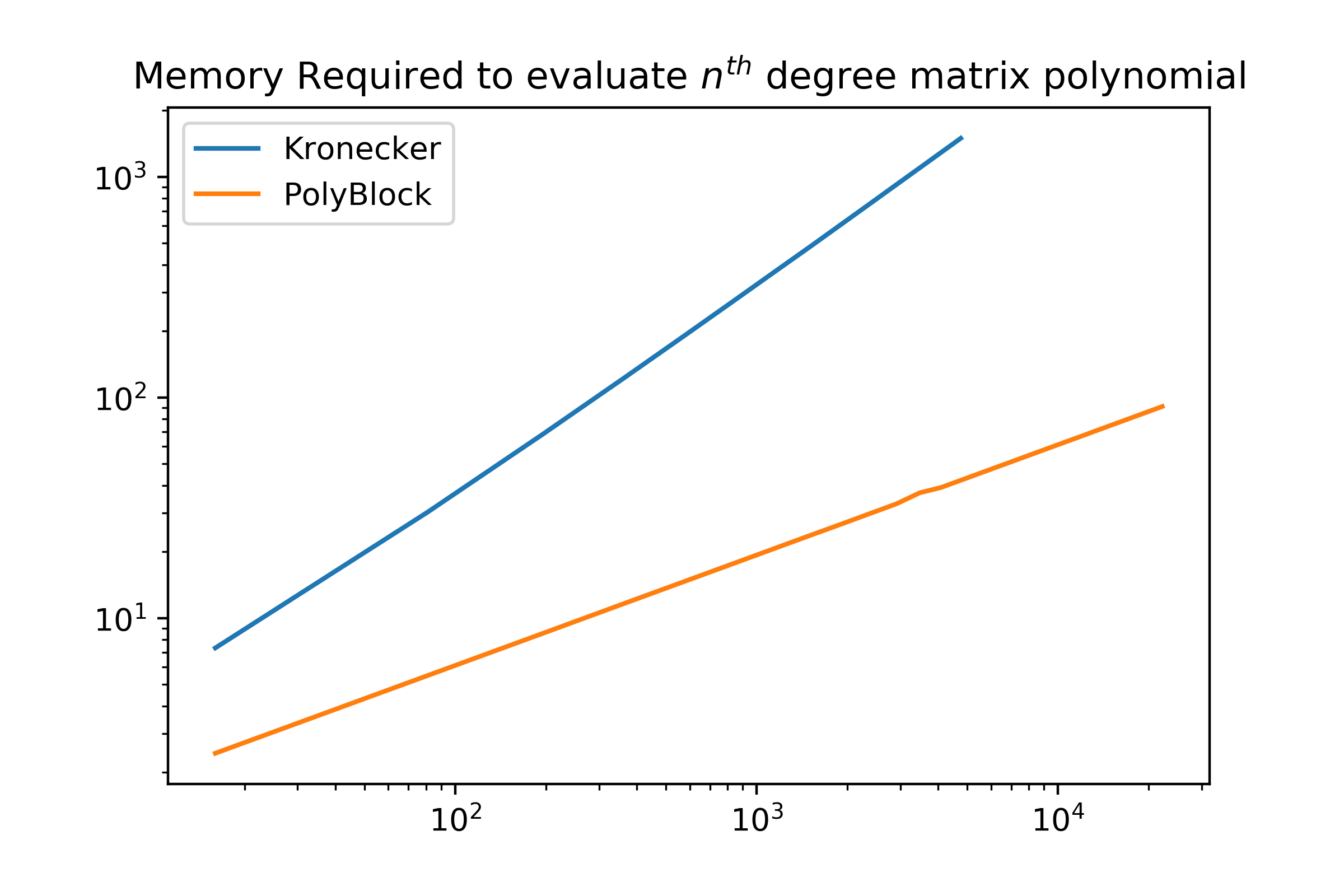
Here we can see two diverging behaviors in memory requirement. This is entirely due to the creation of the middle matrix in the pretty expression that requires $\mathcal{O}(dn^2)$, with $d$ being the degree of the polynomial being evaluated. While the blocked polynomial algorithm only requires $\mathcal{O}(\sqrt{d}n^2)$ storage. My guess as to why the blocked algorithm is increasing in speed relative to the nice expression is that the sheer requirement requires the matrix to be streamed from RAM and not cache, but that is just a guess.