Generating Positive (Semi) Definite Matrices

It has been a while since I have posted an article here, so I will start with something light. Recently, I have been looking at how to tune the weight matrices of a model predictive controller (MPC), which is an advanced process control methodology; click here for an example. We aren’t going to talk about that here (yet), but it motivates what this whole post is about. In effect, there is little information in the literature about tuning the $(Q, R)$ matrices in the control objective $J$ for particular output responses [1,2].

\[\begin{align} J = \frac{1}{2}\sum_{t=0}^\infty \left(x^T_tQx_t + u_t^TRu_t\right) \end{align}\]

I will not get too far into the weeds with control in this post, but in effect, if you tune the $Q$, and $R$ matrices, you get a different optimal feedback law $u_t = -Kx_t$. In many instances, the choice of $(Q, R)$ is fairly arbitrary and is not based on real-world economic costs or weights but is chosen to get a particular feedback response in effect, $u_t = -K(Q, R)x_t$. I have been looking at how to sample the space of plausible matrices to understand better the map of $(Q, R) \mapsto K$, via the DARE equation [3]. However, not any matrix will do; $ Q$ and $R$ need to be at least positive semidefinite (PSD), meaning all the eigenvalues must be positive. There are a couple of different approaches to generating these matrices, but some have better properties than others.

1) Rejection Sampling

I think the simplest possible way to sample is to start with rejection sampling, e.g., generate a sample from an easy-to-sample domain (the set of all matrices) and then check if it is inside the object we want to sample from (PSD matrices).

import numpy

def make_PSD_rs(n:int):
    while True:
        Q = numpy.random.rand(n,n)
        Q_ev = numpy.linalg.eigvals(Q)
        
        if min(Q_ev) >= 0:
            return Q

However, as with every time a rejection sampling approach is utilized sampling efficiency (the number of matrices we need to generate before we get a valid PSD matrix). Here, as we get into larger and larger matrix sizes, we need to generate exponentially more random matrices to find a PSD matrix by happenstance/ rejection sampling. In addition, the requirement to find the eigenvalues of these randomly generated matrices is a large burden on the same computational cost of generating a PSD matrix via the other methods presented here.

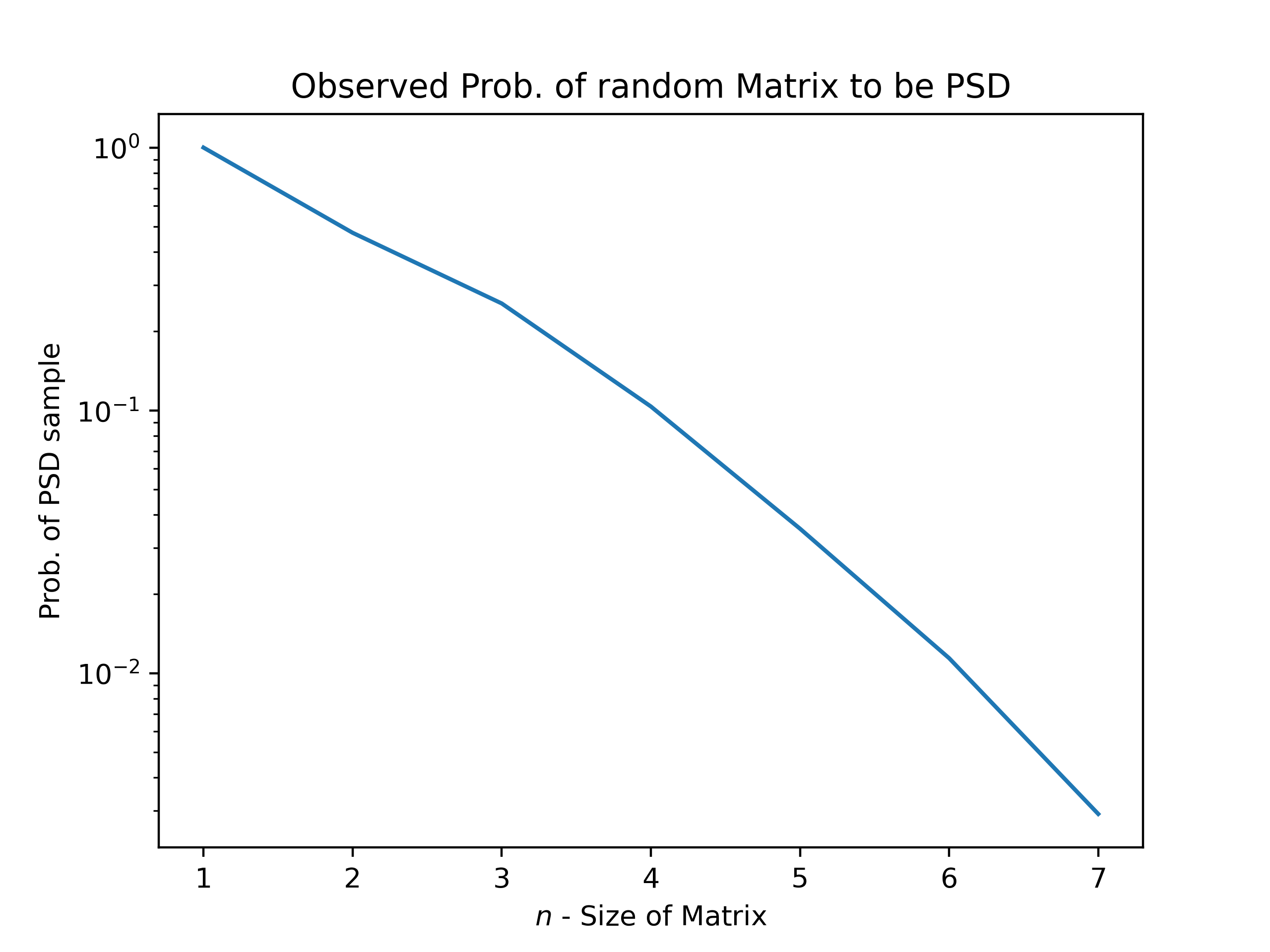
We also see that the eigenvalue distribution of the sampled matrices is not at all uniform.

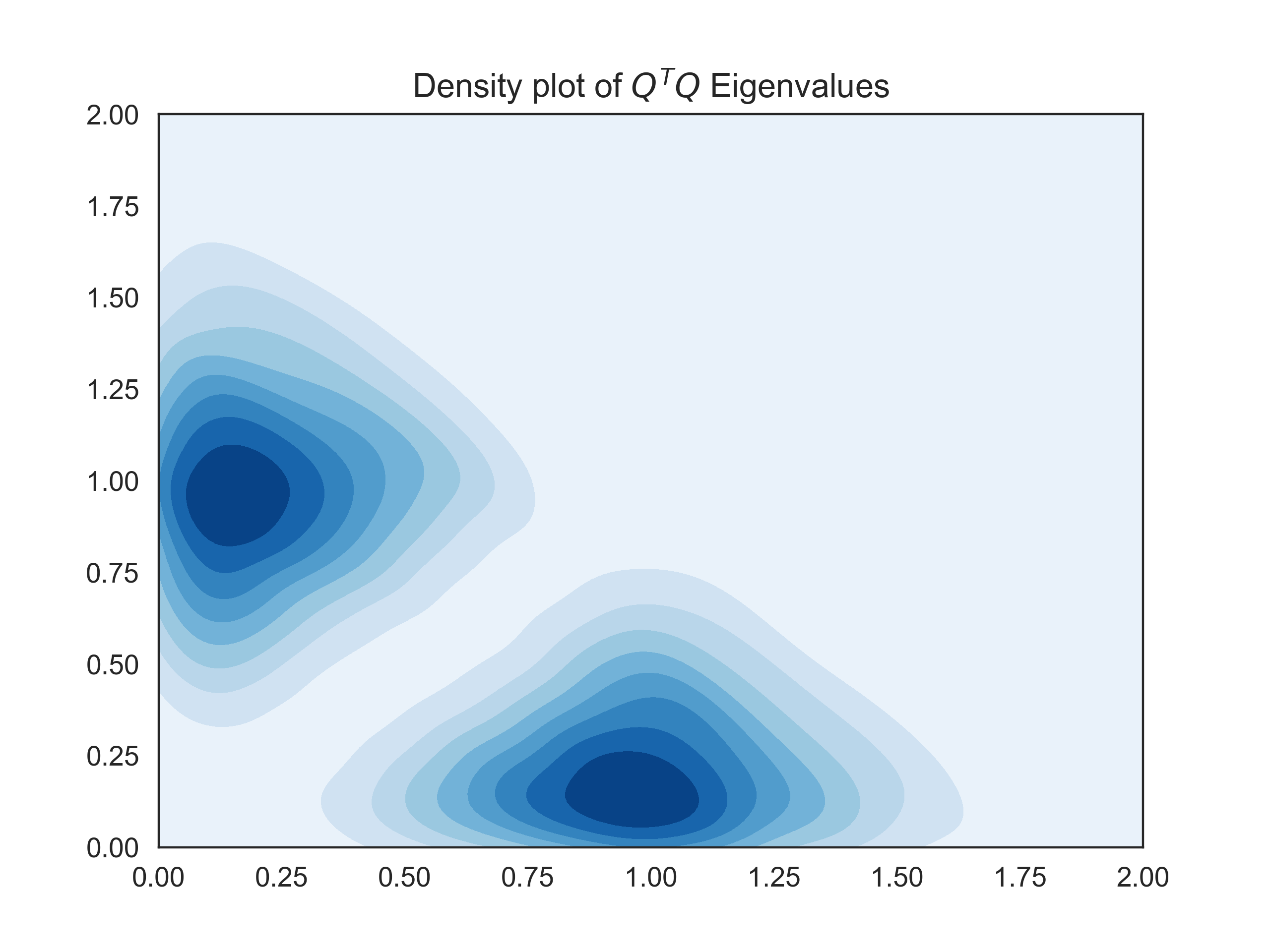
2) Matrix Product Generation

Another simple way to make a matrix is to rely on a simple property of PSD matrices is that every single one can be generated as a product of two matrices e.g. pick any $Q$, then $Q^TQ$ is a positive definite matrix (assuming Q is real). A small snippet of Python code shows the realization of this approach. This is exponentially more efficient than the last method for larger-sized matrices [4].

import numpy

def make_PSD_product(n:int):
  Q = numpy.random.rand((n,n))
  return Q.T@Q

However, this approach is not uniform in the sense that it does not uniformly sample from the space of matrices. We can see a consequence of this in the following plot. Where we look at the eigenvalues of the matrix we generated via $Q^TQ$.

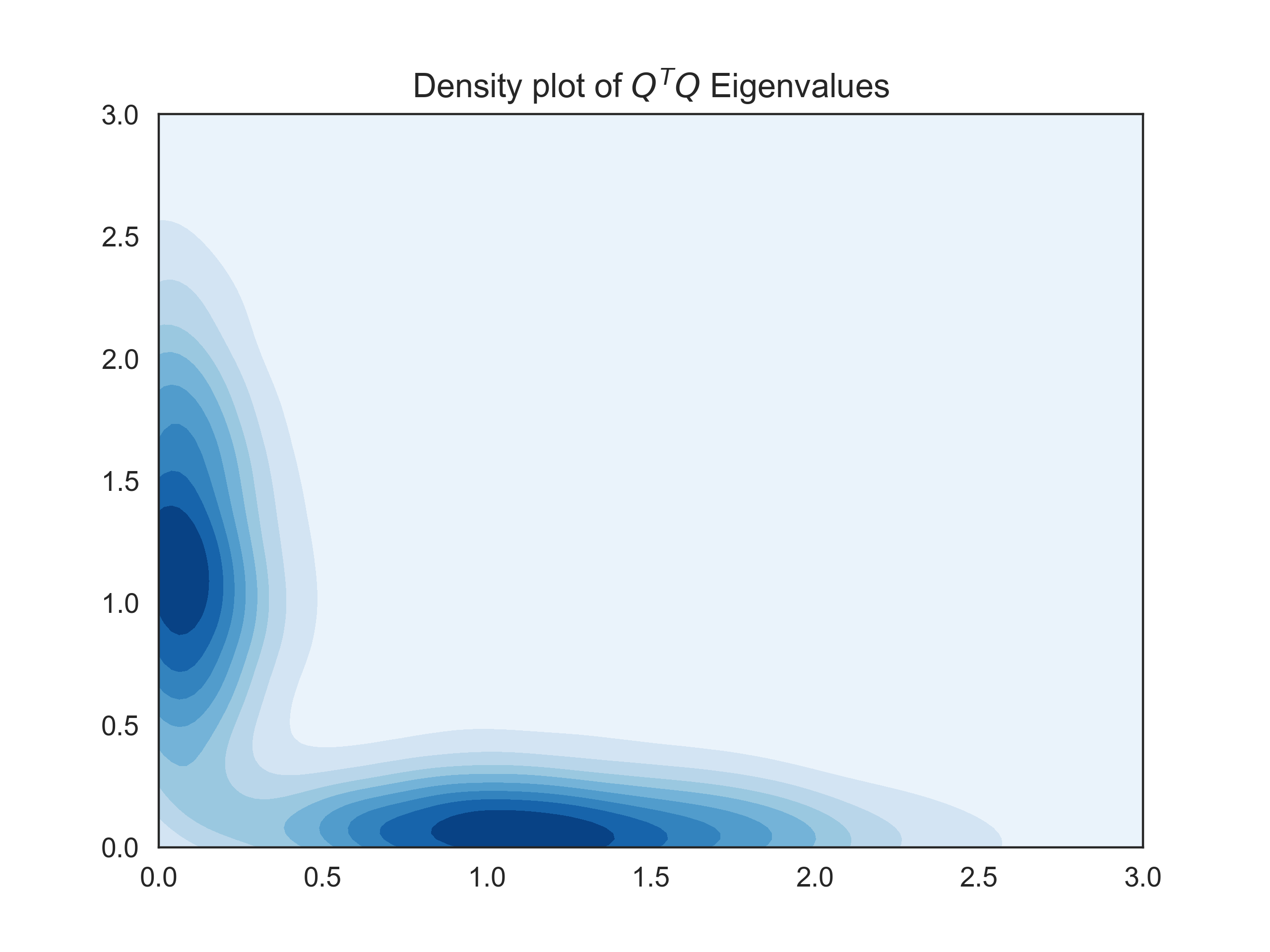
3) Eigenvalue Generation / Direct QR Approach

A somewhat more complicated approach is by generating matrices with placed specified eigenvalues. This method allows for us to specify the exact distribution of the eigenvalues of the PSD Matrices we are generating and can be made directly with common linear algebra tools. This recipe requires the generation of an orthogonal matrix, which we can make by taking the Q part of the QR decomposition of a random matrix or by doing the Gram-Schmidt orthogonalization procedure on a random matrix. Gram-Schmidt is a topic we have previously covered and can be accessed here. For simplicity, we will be utilizing the QR method, as this is the simplest to implement here.

def make_PSD_qr(n:int):
    evs = numpy.random.rand(n)
    P = numpy.random.rand(n, n)
    Q, _ = numpy.linalg.qr(P)
    return Q@numpy.diag(evs)@Q.T

As we have placed the eigenvalues directly from a random uniform distribution, we know they are uniformly distributed. This is one of the least spoken about methods to generate PSD Matrices, but literature backs the uniformity of the sampling of random orthogonal matrices (and is how Scipy generates orthogonal matrices under the hood)[5,6]. This method can also be extended to generate random matrices with eigenvalues from particular distributions.