Chebyshev Ball of a Polytope

The Chebyshev ball is the largest ball that fits inside of a set $\mathcal{Q}$. There is a different definition for this: the smallest ball that contains the set $\mathcal{Q}$. The second definition is fundamentally different from the first definition, and we will only cover the first definition. The first definition is a simple statement that can be written as the following optimization problem. We can read this as “maximize the radius of the ball subject to the ball fitting in $\mathcal{Q}$.”

The above formulation lets us state the problem, but the formulation is not helpful to solve the problem. I will cover the case of $\mathcal{Q}$ being a finite-dimensional polytope. In addition $\mathcal{Q}$ is a set constrained by a finite number of hyperplanes of the following form $a_i \cdot x \leq b$. This is what you would normally think of the polygon. If it we did not have a finite number of hyperplane contraints, then while it would be convex it would not be solvable in the following way (Think of a circle). Mathematically this is expressed as the following set $\mathcal{Q} = {x\in\mathcal{R}^n: Ax\leq b}$. Below is an example of a Chebyshev ball of a polytope.

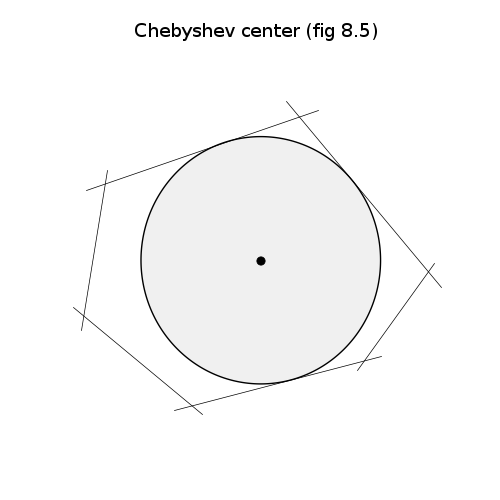
Here I will give a quick sketch of how to reformulate the first optimization problem into a simple linear program for the polytopic region $\mathcal{Q}$. This derivation is found on slide 12 in the references. The first step is separating the center of the ball and the area around the ball.

Here the statement $ x_c + u \in \mathcal{Q}$ means, everything in the set $u$, which is the ball of radius $r$ centered at zero shifted by the center $x_c$ is inside our polytope. The second line expresses the hyperplane constrains of the polytope, $\mathcal{Q}$. All points $y\in\mathcal{Q}$ must obey the constraints $Ay\leq b$, where there are $m$ hyperplane constraints. Since this ball must be inside the polytope then so must $x_c + u, \forall u : \left \lVert u\right\rVert_2 \leq r, i\in 1, \dots, m $. The last line is a rearrangement of the previous line. They are then recasting it to find the most extreme point of the set $u$ that would violate the constraint. Instead of needing to look at all points in $u$ we need to know the largest value that it could attain. This reformulation can is completed via the Cauchy-Schwartz Inequality.

We can reformulate this optimization problem from the first one based on balls into the following simple LP. I like writing things in minimization, so I am multiplying the objective by $-1$.

Via similar arguments, we can show that if $\mathcal{Q}$ has equality constraints, it takes the following form. Where $\mathbf{I}$ is the set of equality constraints, $\mathbf{J}$ is the set of inequality constraints of the region $\mathcal{Q}$.

I have written up this reformulation in Python, and it utilizes my SimpleDenseGurobi package. The package allows us to express and then solve the optimization problem quickly. Please play around with the code!

Code Listing

def chebyshev_ball(A: numpy.ndarray, b: numpy.ndarray, equality_constraints: Iterable[int] = None,
                   bin_vars: Iterable[int] = None, deterministic_solver='glpk') -> Optional[SolverOutput]:
    """
    Chebyshev ball finds the largest ball inside of a polytope defined by Ax <= b
    This is solved by the following LP

    min{x,r} -r

    st:
            Ax + ||A_i||r <= b

            A_{eq}*x = b_{eq}

            r >=0

    :param A: LHS Constraint Matrix
    :param b: RHS Constraint column vector
    :param equality_constraints: indices of
    rows that have strict equality A[eq] @ x = b[eq]
    :param bin_vars: indices of binary variables
    :param deterministic_solver: The underlying solver to use, eg. gurobi, ect
    :return: the SolverOutput object, None if infeasible. The radius is the last number in the solution of the solver object if it is feasible
    
    """

    if bin_vars is None:
        bin_vars = []

    if equality_constraints is None:
        equality_constraints = []

    c = numpy.zeros((A.shape[1] + 1, 1))
    c[A.shape[1]][0] = -1

    const_norm = constraint_norm(A)
    const_norm = make_column(
        [const_norm[i][0] if i not in equality_constraints else 0 for i in range(numpy.size(A, 0))])

    A_ball = numpy.block([[A, const_norm], [c.T]])

    b_ball = numpy.concatenate((b, numpy.zeros((1, 1))))

    if len(bin_vars) == 0:
        return  solve_lp(c, A_ball, b_ball, equality_constraints, deterministic_solver=deterministic_solver)
    else:
        return  solve_milp(c, A_ball, b_ball, equality_constraints, bin_vars, deterministic_solver=deterministic_solver)

Resources

• Equation Derivation Source